Aで割るとBあまり

一番大きいのを見つけて、その約数の中から、３の倍数で奇数のものを探せばいい。
一番大きいのをどうやって見つけよう。
１１５７３ー２３＝１１５５０
６９４０ｰ１０＝６９３０
Aは、１１５５０も６９３０も割りきれる数(またはその約数）だ。
１１５５０と６９３０の最大公約数をまず求めてみる。→考え方

最大公約数は２３１０

「問題は、Aは３の倍数でしかも奇数です。」と書いてあります。
では、Aの中で最大の数(奇数）は何でしょう。

この約数の中で最大の奇数は１１５５

最大公約数の２３１０を利用して考えてみましょう。
求める数は奇数ですから、２３１０を２で割って見ましょう。
２３１０÷２＝１１５５
これで奇数ができました。
この約数の中で、3の倍数で、余りの２３よりも大きいものを探せば、それがAです。

Aを調べてみるとAは５個

１１５５を素数に分解してみましょう。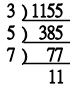

３の倍数ですから３はAの約数の中に必要です。
そこで、１１５５を３以外の数で順番に割ってみましょう。
１１５５　　　　・・・・①
１１５５÷５＝２３１　・・・・②
　２３１÷７＝　３３　・・・・③
　２３１÷１１＝２１　（これは２３より小さいからAではありません）
１１５５÷７＝１６５　・・・・④
　１６５÷１１＝１５（これも２３より小さい）
１１５５÷１１＝１０５・・・・⑤
この5つを小さい順に並べると
３３，１０５，１６５，２３１，１１５５
この５個がAです。
最初から素数に分解して、答を見つける方法もあるでしょう。