Aで割るとBあまり

一番大きいのを見つけて、その約数の中から、３の倍数で奇数のものを探せばいい。
一番大きいのをどうやって見つけよう。
１１５７３ー２３＝１１５５０
６９４０ｰ１０＝６９３０
Aは、１１５５０も６９３０も割りきれる数(またはその約数）だ。
１１５５０と６９３０の最大公約数はいくつだろう。

最大公約数は２３１０

これをユークリッドの互除法で解いてみよう。
大きい数字を小さい数字で割ります。
商が１なので、実際は引き算だけで計算できます。

次に割る数６９３０を、余りの４６２０で割ります。

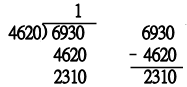
これも商が１ですから、引き算で計算できます。
さらに、割る数４６２０を２３１０で割ります。

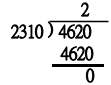
これも引き算でできますし、数字を見れば割り切れることが分かります。
こうして割り切れたとき、割った数の２３１０が、最大公約数です。
でも、「問題は、Aは３の倍数でしかも奇数です。」と書いてあります。
では、Aの中で最大の数(奇数）は何でしょう。
最大公約数の２３１０を利用して考えてみましょう。

考え方へ進む