図のように、輪ゴムを立方体の箱にかけます。
・輪ゴムは立方体の辺と直角に交わる
・向きが同じ輪ゴムは重ならない
このとき、かけた輪ゴムどうしの交点の個数について考えます。
例えば、3本の輪ゴムを右の図のようにかけた時、交点は4個です。
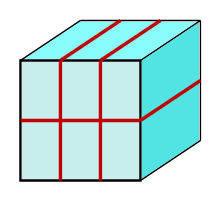
・輪ゴムは立方体の辺と直角に交わる
・向きが同じ輪ゴムは重ならない
このとき、かけた輪ゴムどうしの交点の個数について考えます。
例えば、3本の輪ゴムを右の図のようにかけた時、交点は4個です。

(3)100本の輪ゴムをかける時、交点は最も多くて何個ですか。
交点の数は、輪ゴムをかける本数を(a、b,c)とすると、(a×b+b×c+c×a)×2だった。このとき、3つの輪ゴムがなるべく等しいとき、交点の数が多くなるんだ。
一つのかけ方ばかり多いと、交点は少なくなる。
そこで、(33,33,34)と輪ゴムをかけるとき、交点の数は一番多くなる。
これは (33×33+33×34+・・・省略・・・)×2 と計算できる。
解答へ進む