図のように、輪ゴムを立方体の箱にかけます。
・輪ゴムは立方体の辺と直角に交わる
・向きが同じ輪ゴムは重ならない
このとき、かけた輪ゴムどうしの交点の個数について考えます。
例えば、3本の輪ゴムを右の図のようにかけた時、交点は4個です。
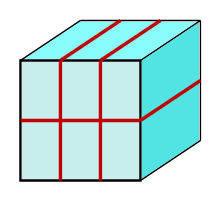
・輪ゴムは立方体の辺と直角に交わる
・向きが同じ輪ゴムは重ならない
このとき、かけた輪ゴムどうしの交点の個数について考えます。
例えば、3本の輪ゴムを右の図のようにかけた時、交点は4個です。

(2)5本の輪ゴムをかけたところ、交点は12個ありありました。
さらに3本の輪ゴムをかけたら、交点は全部で何個になりますか。
最も多い場合と、最も少ない場合の交点の個数を答えなさい。
さらに3本の輪ゴムをかけたら、交点は全部で何個になりますか。
最も多い場合と、最も少ない場合の交点の個数を答えなさい。
まず、最も少ない場合はいくつ?
wakuDisp(); ?> 5本の輪ゴムのかけ方はいろいろある。
上前下後まわりのゴムをA本、上右下左周りのゴムをB本,前右後左周りのゴムをC本として(A、B、C)のように表すと
(5,0、0)
(4,1,0)
(3,2,0)
(3,1,1)
(2,2,1)
の5通りのゴムのかけ方がある。
交点の数は(A×B+B×C+C×A)×2で表される。
だから、交点の数は、
(5,0,0)は、(5×0+0×0+0×5)×2=0
(4,1,0)は、(4×1+1×0+0×4)×2=8
(3,2,0)は、(3×2+2×0+0×3)×2=12
(3,1,1)は、(3×1+1×1+1×3)×2=14
(2,2,1)は、(2×2+2×1+1×2)×2=16
で、交点が12個になるのは、(3,2,0)
最も少なくなるのは、交点が少ない方が良いのだから
(3+3,2,0)と、3本の平行な輪ゴムに平行に、もう3本輪ゴムをかける場合です。交点を計算しましょう。
解答へ進む