比の価(ひのあたい)ってなに
÷のかわりに:を使う国があるそうです。そんな国では、2:3というのは、2÷3という意味です。
この計算の商、つまり答えが、比の値です。
| ここでは2÷3を計算して、 | 2 | が比の値です。 |
| 3 |
となりますので、分数で書いた方が簡単です。
比の値の意味
比の値は、後ろの数が1のとき、前の数はその何倍かを示す数です。
例えばある時間の、棒の長さと陰の長さを考えます。
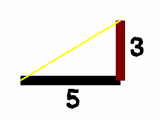
ある時刻の棒の長さが3mのとき、陰は5m
比で書くと 3:5
比の値は、3/5(5分の3)
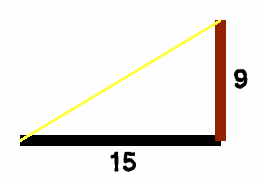
棒の長さが9mのとき、陰は15m
比で書くと、 9:15
比の値は 9÷15=3/5(5分の3)
比の値は同じなのです。

棒の長さが3/5mのとき陰の長さは1mです。
後ろの数値が1のときの、前の数値が比の値なのです。
比の値の利用
比の値は,分数で書くと| 3 |
| 5 |
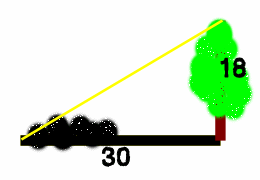
| 30× | 3 | =18 |
| 5 |
後ろの数値が1のときに、前の数値はいくつかというのが比の値。
別のいい方をすると、前の数は後ろの数の何倍になるかを表すのが比の値です。
傾きが3/5(5分の3)
またこれは、グラフにすると、3/5(5分の3)という傾きも表しています。右に5進んで、上に3上がる傾きを表しているのです。
どちらの黄色い線の傾きも同じで5分の3なのです。
使いながら、比の値なれましょう。
では 比の値 を計算してみよう
比の値ドリル平成10年以前は小学校で扱っていた内容です。
平成10年12月14日に発行され、平成14年4月1日から施行した小学校指導要領では、
「(8) 内容の「D数量関係」の(1)については,具体的な場面を通して数量の関係を調べ,
等しい比があることを理解する程度とするとともに,
比の値は取り扱わないものとする。」
となっています。
ということで、教えなくてもいい内容した。
他によく似た内容に、、1当たりの量とか割合という学習があります。
これが平成27年度には
「取り扱わない」という以前の(8)の項目が削除され・・・
ということは、また学習することになりました。
内容は増えたり減ったりしていますが、
もりの学校はそれにとらわれずいろいろな学習ができるようにしていきます。
内項の積と外項の積が等しいことも、扱った方が良いのかなぁ?これは中学校で比の解き方の主流となっているのでしょうか?
(ページエラー誤字報告がありましたが見つかりません。
再度前後の文を入れて報告をお願いできますか?)