再帰(さいき）と三角形　

同じようなプログラムを重ねることを多重ループといいます。
多重ループは、力業（ちからわざ）でかっこ悪い、もう少し旨くかけないかと言うときに、再帰を使います

ここにあります

今回のブロックは引数（ひきすう）のあるブロックです
作り方を説明すると
まず、ブロックを作るを押（お）して

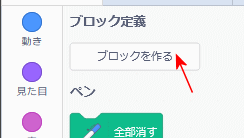
次に
０，名前を「三角形」（さんかっけい）と書いて、
１，引数を追加（ついか）を押（お）して
２，引数の名前のところへ、「辺（へん）の長さ」とかいて
３，OKを押します

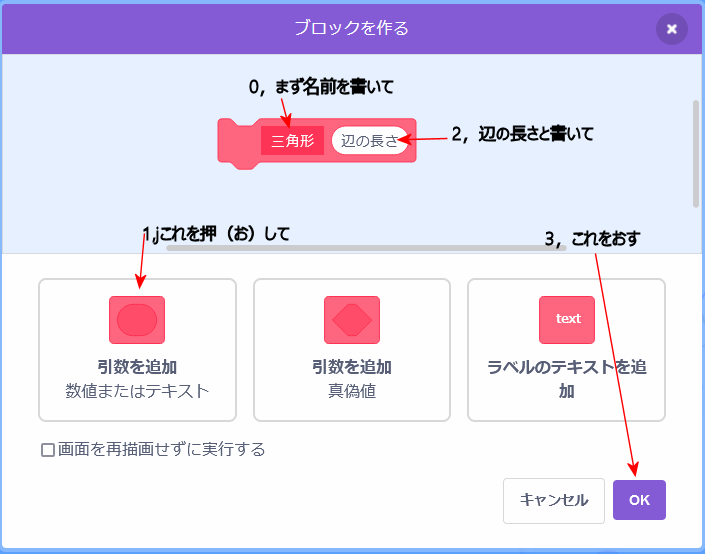
これで、引数付きのブロックが出来ます。
引数はたくさんつけれるはずですが、ここでは1個だけ。

まず、三角形1つを書いてみましょう

こんなふう
ああ～～今気がついたんだけど
（全部消すと、ペンを下ろす）を（ｘ座標をー１００ｙ座標を－１２０）の下にすると、変な線が出ません。

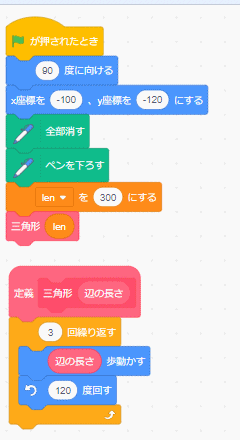
これは普通の定義（ブロックとも言う）の呼び出し。
ブロックを呼び出すときに、このブロックは、辺の長さをブロックに渡します。

再帰というのは、ブロックの中にブロックを書くこと
下のようにやってみよう。

おや
一つ三角形を書いて
次に、長さを半分にして、また三角形を書いて
次に長さを又半分にして、三角形を書いて
どんどん書いて・・・でもとまらない。

これで、どうだ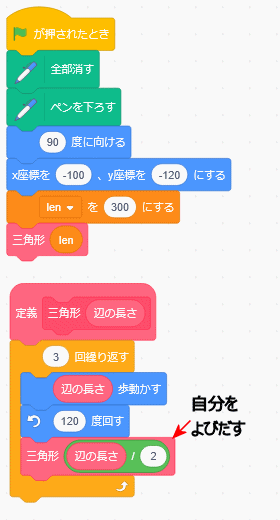

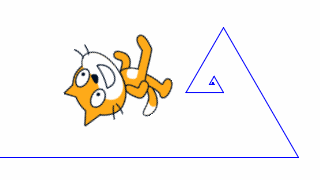
あれ、三角形を書かずにどんどん小さくなっていく
それに止まらない

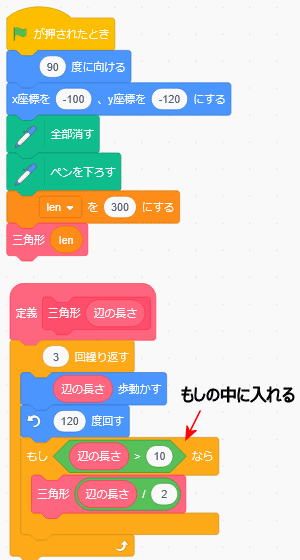
lもしの中に入れると、那賀産がどんどん小さくなっていって、10より小さくなったらもう止めだ
再帰はその再帰の中に、ストップするところを入れないといけない
これは、「もし辺の長さ>10」でないときはなにもしないでもどるから、次の再帰に進まないんだ

まず最初の定義(ブロック)は、長さが300で動き長さを半分(150）にして、定義を呼び出す		これで再帰が終了する
↓		↑
２番目の定義は、長さが150で動き長さを半分の75にして、定義を呼び出す		前の定義にもどる
↓		↑
３番目の定義は、長さが150で動き長さをにして、定義を呼び出す		前の定義にもどる
↓ これを繰り返して ↓		↑
N番目の定義で、長さが10より小さくなったとき次の定義は呼び出さないで終わる	→	終わったから前の定義にもどる

できた

う～～ん
色々あると思うけど、ボクの知ってるのは
最大公約数を求める（ユークリッドの互除法）しか思いつかない。
たぶん、迷路を作るとか、色で塗りつぶすとか、も使うと思う。
いろいろプログラムをしていく内に出てくるだろう。

こんな図形は、フラクタルって調べると色々出てくるだろう
調べて作ってみてください。

次へ進む