円すいの側面積

解答１　中心角を求めて

画像を小さくして、大きな円を描いてみました。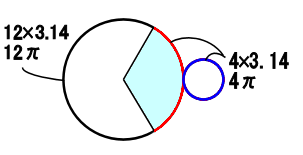

底辺になる円の円周は、４×３．１４
おうぎ形の赤い部分といっしょです。
おうぎ形を含んだ大きな円の円周は、半径が６ｃｍだから１２×３．１４です。
これは、赤いおうぎ形の弧の長さのちょうど３倍です。

そこで、中心角も３６０°の３分の１で、３６０×	１	＝１２０°
	３

水色をぬったところの面積は
大きな円の面積の３６０分の１２０だから

６×６×３．１４×	１２０	＝１２×３．１４
	３６０
		＝３７．６８

中心角を使わなくても、おうぎ形の弧の長さは、円周の三分の１だから
面積も３分の１で

６×６×３．１４×	１	＝１２×３．１４
	３
		＝３７．６８

答、３７．６８ｃ㎡
πを使えば

６×６×π×	１	＝１２π
	３

となります。

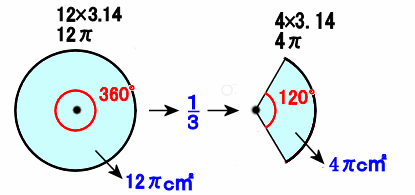
円周の長さが３分の１なら、中心角も３分の１、面積も３分の１になります。
他の方針も見てみよう
一つは、円の中心角を求めて計算する方法。
もうひとつは、
扇形の半径と弧の長さで計算する方法。


もうひとつは、
扇形の半径とその中心線の長さで計算する方法。