たーレスの定理

正解です　正解は　90です。

赤い点で示した角度は何度でしょう。

中心角の半分だから
90°です。

これは、ターレスの定理といいます。
「円周上に三点がある三角形のうち（外接円）、三角形の一辺が直径になっているものは、
すべて直角三角形である。」というものです。

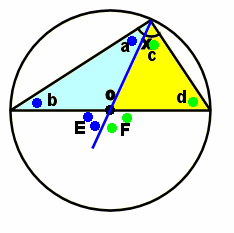まず a=b です。だって、直径を二辺とする、二等辺三角形だもの。 だから、 E=a+b=2a 同様に ｃ＝ｄ です。これも、二等辺三角形だものね。 だから F=c+d=2c ｘ＝ａ＋ｂ だから Ｅ＋Ｆ＝２（ａ＋ｂ）＝２ｘ となります。 Ｅ＋Ｆは、直線だから Ｅ＋Ｆ＝１８０° ｘはその半分で９０°です。

「円周角の定理から、角ｘは、１８０°の半分の９０度」
って言っちゃえば、証明はそれだけで終わりで、簡単ですけれどね。
で、この定理をターレスの定理って言います。
ターレスは、数学の神様といわれています。
数学を通じて、いろいろな出来事を、証明していくという方向で見始めた人なのです。
こういう証明という方法は、ギリシャで考え出されました。
それ以来だんだん
「神様が言ったり偉い人が言ったりするから正しいんじゃなくて、証明されて正しいといえる。」
という考え方が、世の中の考え方になってきたのです。
裁判でも、しばらく前までは
「何を言った。証言した。」
ということが重視されていましたが、最近はだんだん
「証拠がある、そこからきちんと証明できる。」
ってことが重視されるようにだんだんなってきています。
算数はそんな世の中の考え方にも、大きく影響しているのです。
「何を言ったか。」
もとっても重要だけれど、それ以上に
「何をやったか。」ってことが大事だという世に中に向かっているのです。
次問題へ進む