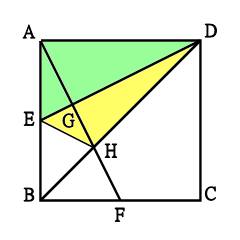
下の図のように、一辺の長さが30cmの正方形ABCDにおいて
点E,Fはそれぞれ辺AB、BCを二等分する点とします。
直線DEと直線AFの交わる点をG、直線BDと直線AFの交わる点をHとするとき
①②の面積をそれぞれ求めなさい。(開成中2013年入試 改題)
①三角形HBF点E,Fはそれぞれ辺AB、BCを二等分する点とします。
直線DEと直線AFの交わる点をG、直線BDと直線AFの交わる点をHとするとき
①②の面積をそれぞれ求めなさい。(開成中2013年入試 改題)
②四角形GEBH


①の面積は、30×15÷2÷3=75平方cmです。
②四角形GEBHの面積は
さてこれはどうしましょう。三角形AEGの面積が分かればできそうですね。
三角形AEDと三角形DEHの面積を求めて
この三角形の面積の比が、辺AGと辺GHの比になる。
それを使って、三角形AEHの面積を、その比で分ければ、三角形AEGの面積が出る。
そうすれは、あとは引き算でできるね。
三角形AEDの面積は、30×15÷2=225平方cm
三角形DEHの面積は 三角形DEBの面積から三角形BEHの面積を引けばいいから
225-75=150平方cm
二つの三角形は、辺DEを底辺とする三角形と考えると、
この面積の比が辺AG:辺GHと同じだから
辺AG:辺GH=225:105=15:7
これを使って、三角形AEGの面積が出れば、あとは簡単。
②の四角形GFBHの面積は・・・何平方センチメートルだろう。
次へ