ピタゴラスの3数
直角三角形の3辺になるような3つの整数の組をピタゴラスの3数といいます。
例えば(3,4,5)がピタゴラスの3数で
3×3+4×4=5×5 となっています。
他にも次のようなピタゴラスの3数があります。
|
左を2倍にしたもの |
左を3倍したもの |
||

|
(3,4,5) |
(6,8,10) |
(9,12,15) |

|
(5,12,13) |
(10,24,26) |
(15,36,39) |

|
(7,24,25) |
(14,46,50) |
(21,72,75) |

|
(8,15,17) |
(16,30,34) |
(24,45,51) |
n×m
(m×mーn×n)÷2
(m×m+n×n)÷2
例えば、5,3を入れると
3×5=15
(5×5ー3×3)÷2=8
(5×5+3×3)÷2=17
として、8、15,17というピタゴラスの3数になります。
参考文献「0から100までの数」、山崎直美著、さ・え・ら書房
さて、でもこうならない数はどうするんだろう
たとえば
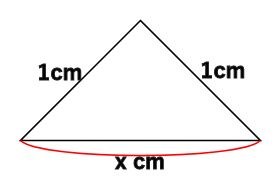
このxの長さは数字で表せないんでしょうか。
分数で
もどる