下の図の長方形ABCDにおいて、BEとDHは平行で、
CEとBD,DHの交点がF,Gです。
三角形BFGの面積が8c㎡ のとき、
次の問に答えなさい。
(1)FG:GCの長さの比を求めなさい。
(2)ABの長さを求めなさい。
鴎友学園女子中学 2009年
CEとBD,DHの交点がF,Gです。
三角形BFGの面積が8c㎡ のとき、
次の問に答えなさい。
(1)FG:GCの長さの比を求めなさい。
(2)ABの長さを求めなさい。
鴎友学園女子中学 2009年

(2)ABの長さを求めなさい。
正解です
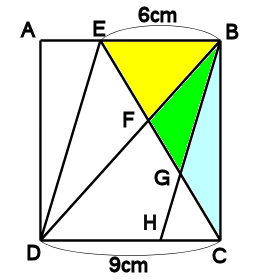
EF:FG:GC=6:4:5 がヒントだね。
くま 緑色の面積が8だから、
6:4:5=X:8:Y として、黄色い面積と水色の面積がわかるよね。
ウサギ 3つの三角形の高さはどれも同じだから、面積の比は、底辺の長さの比になるんだ。
リス X=12,Y=10
3つの面積を足すと、12+8+10=30c.㎡だね。
ウサギ この面積は、EB×BC÷2 だから
30=6×BC÷2 (両辺に2をかけて)
60=6×BC (両辺を6で割って)
BC=10cmだね。
台形と三角の変形