平行四辺形の面積比

東海中学　2001年(一部改訂）
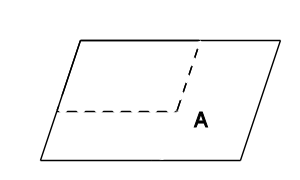
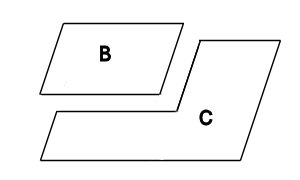
平行四辺形Aを何倍かに縮小した図形Bを作り、
AからBを下図のように切り取り、図形Cを作ります。
２つの図形BとCの周囲の長さを比べたところ、
Bの周囲の長さはCの周囲の長さは０．６倍でした。
このとき次の問に答えなさい。
（１）Bは元の平行四辺形Aを何倍に縮小したものですか。
（２）Bの面積が１２ｃ㎡のとき、Cの面積を求めなさい。

（２）Bの面積が１２ｃ㎡のとき、Cの面積を求めなさい。