台形と三角形の移動

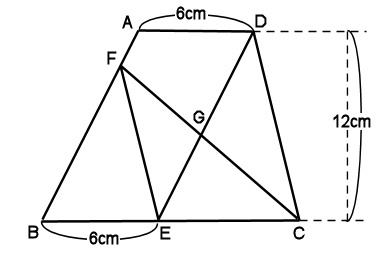
下の図のような台形ＡＢＣＤがあり、 ＡＤ＝ＢＥ＝６ｃｍ、高さ１２ｃｍです。
ＣＤとＥＦが平行で、 ＤＥ とＣＦの交点をＧとしたとき、
ＤＧ：ＧＥ＝５：４でした。
このとき、次の問に答えなさい。
（１）三角形ＥＦＧの面積を求めなさい。
（２）ＣＥの長さを求めなさい。
（３）ＡＦ：ＦＢを最も簡単な整数の比で表しなさい。
桐朋中学　2001年

正解です 正解は16c㎡です。

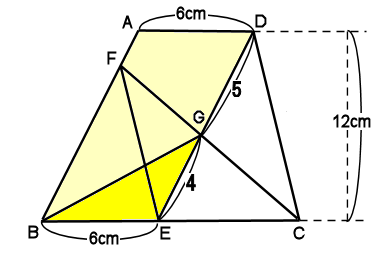
クマ　三角形GFEは、三角形GBEと同じです。
タヌキ　三角形DBEの面積がわかるから、それを５：４に分ければ、三角形GBEがわかるね。
キツネ　三角形BDEは、平行四辺形の半分だから
　　　１２×６÷２＝３６ｃ㎡
タヌキ　それを、５：４にわけると、三角形BGEは、（５＋４）分の４だから

	３６×	４	＝１６ｃ㎡　となります。
		９

三角形BEGは、平行四辺形の９分の４の半分だから、９分の２　と考えて計算してもいいね。
次の問題へ進む