公約数の問題

最大公約数の問題

算数は魔法みたいなものです
魔法を習い始めた勇者は、だんだん魔法を習ううちに、高度の魔法が使えるようになるのです。
同じように、約数の學主も、だんだん高度な方法が分かるようになるのです。

最大公約数を求める方法を5段階に分けて、これから説明しましょう。
１，初診者
２，初級　約数を書き出す
３，中級　すだれ算を使う・・・・これが一番使える
４，上級　何でも使えるユークリッドの互除法
５，上級者になれない中級者と、上級者も使う、抜け道
この5段階です。
あなたも上級魔法使いになりましょう。

公約数の問題（正方形に切る）

最大公約数はこんな問題です
この後これを使って説明します
やってみましょう







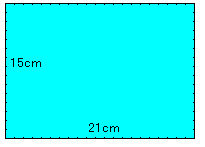
図のような，たて１５㎝、横２１㎝の長方形の中に、同じ大きさの正方形を、すきまのないように、しきつめます。
なるべく大きな正方形をしきつめるには正方形の一辺を何㎝にすればいいでしょうか。

一辺が１ｃｍの正方形だったらどう

■簡単だよ。正方形をしきつめるってことでしょ。
それなら、１辺が１㎝の正方形をしきつめればいい。
▼ちがうと思うよ。
　もっとも大きい正方形でしきつめることができるんじゃないかなあ。

１辺が２㎝の正方形はどう。

１５㎝の辺に並べると，７個並んで，１㎝余っちゃうからだめだよ。

２は、１５の約数ではないから、2cmでわけると、あまるんだね。
15の約数じゃなっきゃダメなんだ。

その１　公約数の魔法を始めたばかりの人に

九九は知っていますか。
九九を知っている人は九九で考えます。
そんな人は「15も21も割れる数は、３だ」「15÷3=5、21÷3=7でどっちも３でわれる」
と気がつくでしょう。
でもここにとどまっていると、大きな数が出てきたときに分からなくなります。

その２　初級魔法　最大公約数を見つける方法その1

１５と２１の約数を書き出してみる

15の約数	１	３	５		１５
21の約数	１	３		７		２１

この2つを比べて見て

15の約数	１	３	５		１５
21の約数	１	３		７		２１
	↑	↑

１と３が公約数で
その中で３が一番大きいから。１５と２１を割れる数、つかり約数でで一番大きいのは３だと分かります。
こんなふうに約数を書き出すと上の図のように最大公約数３が見つかるのです。

１辺が３㎝の正方形で試してみると。

３ｃｍの正方形でうめることができました。

魔法その３　わりざん（すだれざん）で求める

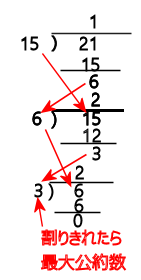
15と21はなんとかなったけどもっと大きい数はどうなの
割る数が見つかるときは、すだれ算という計算で出来ます。
計算で出来るのがすごい・・・というか・・・これが分かっていると頭の中で見つけるときも簡単です。

動画で見てみましょう


もっと大きな数でも簡単にできます
ドリルページを作りますのでそちらで見てください。

この方法の良いところは、最小公倍数も簡単に求められることです

実は、3×5×７としても105となって最小公倍数が出るのです。

ドリル1　すだれ算で最大公約数を求める
ドリル2，すだれ算で最大公約数を求める

魔法その４　ユークリッドの互除法で求める

もっとずっと大きな数だったらどうするんだろう。
こんなときは、コンピュータのプログラムでも使うユークリッドの互除法を使います。
以下のようになります。




こういう計算の仕方を、これを発見した人の名前をつけて、ユークリッドの互助法っていうんだ。

その4解説1　ユークリッドの互除法の説明　大きい正方形から考える。

この中に入る一番大きな正方形は何か考えてみて。
それは15cmの正方形です。
それは、はんぱができるからだめじゃないの。


●このままではだめさ。
　でも、残りの長方形を正方形でしきつめることができれば、
　同じ正方形で、一辺が１５㎝の正方形もしきつめることができるんだ。
▼どうして

その4解説2　残りを敷き詰めると

■　どういうこと、わかるように説明してよ。
●　たて１５㎝・横６㎝の長方形の上に並ぶ正方形は、たて１５㎝の長さにあまりが無いようにならんでいる。
縦１５㎝に並べば，横１５㎝にも並ぶから，一辺１５㎝の正方形に並ぶことができる。

■それなら、たて１５㎝横６㎝に並ぶ正方形が見つかれば，それが答えになるね。
▼問題が簡単になったね。数字が小さくなったよ。

その四回説３　こうして、問題は簡単になるんだ

▲今度は、残った長方形を，同じように大きな正方形を考えて、一辺が６㎝の正方形に切ったらどうだろう。
■１５ｃｍの正方形を入れたみたいにするんだね。

●残りはたて３㎝横６㎝の長方形だね。
▲黄色に入る正方形は，緑色の正方形もうめれるんだね。
●そうだよ。さっきと同じように考えるんだ。
黄色の一辺６ｃｍにならぶ正方形は，一辺が６ｃｍの緑色の正方形にも，きちんとならぶわけだ。

■たて３㎝横６㎝の長方形がのこった。
　このの中に並ぶ正方形は・・・・一辺が３㎝の黄色い正方形だ。

その4解説5　元にもどって考えると

黄色に敷き詰められる正方形は
緑色にもしきつめられて
緑色に敷き詰められれば、にず色にも式つけられる。

●本当に一辺が３㎝の正方形が、たて１５㎝横２１㎝の長方形に並ぶか図に書いてみたら，書けたよ。
●この問題は、縦２１と横１５の最大公約数を求める問題なんだ。
　最大公約数を求めるには、こうやって、だんだんわり算して、簡単にして求める用法もあるんだよ。

もう一度　まとめて書いてみると。

こういう計算の仕方を、これを発見した人の名前をつけて、ユークリッドの互助法っていうんだ。
▼この問題は，縦の長さと横の長さの最大公約数を見つければ良いんだ。

これもドリルを作ってみよう←制作中

その5　抜け道

16と21の約数が分からないときは引き算します
21-16=6
この6の約数、1,2,3,6の中に最大公約数があります。
こんな引き算が役に立ちます

３６と４５の最大公約数は　　45-36=9　この場合は9が最大公約数ですぐ分かります

１８と２４の最大公約数　24-18=6　この場合は6が最大公約数です。

42と56の最大公約数は　56-42=７　この場合も7が最大公約数です。

こうやって引き算が役に立つこともあるのです・・・これはユークリッドの互除法の応用です。

64と７２の最小公倍数、公約数　
もどる