(問 1/7)
家から学校までと家から図書館まで、距離を比べました。
家から学校までは4km家から図書館までは5kmです。
家から図書館までは家から学校までの何倍でしょうか。
家から学校までと家から図書館まで、距離を比べました。
家から学校までは4km家から図書館までは5kmです。
家から図書館までは家から学校までの何倍でしょうか。
倍の計算
図を縦(たて)に見ても、倍はかくれています。比べる量をもとになる量で割ると、倍が現れるのです。
| もとになる量 家から学校まで |
1 |
|
4 |
|
|||||
| 5÷4=1.25 | ←ここにも倍がかくれています |
||||||||
| 比べる量 家から図書館まで |
1.25 |
|
5 |
|
5km÷4km=1.25 です。 5の中には4が1.25ある、ということです。 これを1.25倍というのです。 |
||||
簡単に書くと
考えるときは簡単な図が書けると良いですね。
| もとになる量 家から学校まで |
1 |
|
4 |
|
|||||
| 比べる量 家から図書館まで |
1.25 |
|
5 |
|
そこで図を省略(しょうりゃく)すると
| もとになる量 家から学校まで |
1 | 4 | |||
| 比べる量 家から図書館まで |
1.25 | 5 |
どこを計算したら1.25が出るでしょうか。
| 1 | 4 | ||
| 5÷4 | ←ここでも | ||
| 1.25 | 5÷4 | 5 | |
| ↑ここでも計算できます。 | |||
グラフにすると
この関係を正比例のグラフにできます。正比例はだんだん習いますが、ちょっとだけ学習してみましょう。
| 家から図書館まで | 5÷4=1.25 | ||||||||
| 5 | 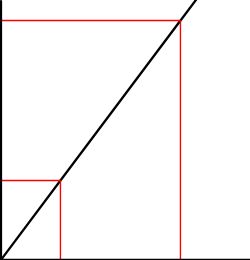 |
||||||||
| 1.25 | |||||||||
| 0 | 1 | 4 | 家から学校まで | ||||||
4を4でわって1になり、
同じように、5を4でわっても1.25倍が出るのです。
このとき、斜めの線を傾き1.25といいます。
傾きは 5/4(4分の5)と分数で表すこともあります。
問題1_クリアです
おめでとう
見直す
次の問題へ進む