図のように三角形PQRの辺上に点A,B,C,D,E,Fをとり、そのうち2点を結んで三角形PQRの辺に重ならないような直線を引きます。このとき、次の問いに答えなさい。
(1)このような直線は何本引けますか?
(2)三角形PQRの内部では交わらないような2直線の選び方は何通りありますか。
(甲陽学院中 平成6年 第2日-5)
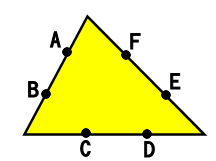
(2)三角形PQRの内部では交わらないような2直線の選び方は何通りありますか。
正解です 正解は51通りです。
タヌキ 12本の中から2本を選ぶのなら12×11÷2=66通りだよ。
リス そこから、重なっているのを引けばいい
クマ 重なっているのを数えると、まずAから線を引いて
ACに重なるのは、3本
ADに重なるのは 4本
AEに重なるのは 3本
AFに重なるのはないから、10本あるよ。
タヌキ 次は、Aを抜いて、Bから線を引いて
BDに重なるのは 2本
BEに重なるのも 2本 合計4本
キツネ 次は、ABを抜いてCから線を引いて
CEに重なるのが1本
ウサギ 全部たして 10+4+1=15通り重なる引き方がある
だから 66-15=51通り
リス 計算でもできるよ。
重なるのは、6つの点から4つの点を選ぶ場合の数と同じだ。
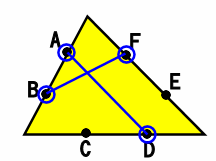
ほら、4つの点を選べば、交わる線が一通りできる。
だから、6つの点から4つの点を選ぶには(組み合わせ)
6×5×4×3÷(4×3×2×1)=15通り
66-15=51通りだ。
次は2つのさいころ