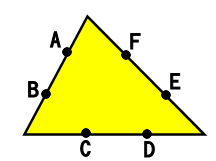
図のように三角形PQRの辺上に点A,B,C,D,E,Fをとり、そのうち2点を結んで三角形PQRの辺に重ならないような直線を引きます。このとき、次の問いに答えなさい。
(1)このような直線は何本引けますか?
(2)三角形PQRの内部では交わらないような2直線の選び方は何通りありますか。ただし、三角形PQRの辺上の点はこの三角形の内部の点としません。
(甲陽学院中 平成6年 第2日-5)
(1)このような直線は何本引けますか?
正解です 正解は12です。
クマ 書き出してみようまずAから引ける線は
AC,AD,AE,AF の4本
Aを除いて、Bから引けるのは
BC、BD,BE,BFの4本
Cからは
CE,CF 2本
Dからは
DE,DF 2本
これで全部たすと、4+4+2+2=12通り
タヌキ もっちかんたんにできるよ
BからもCからもDからも、6つの点のどれからも4本引けるから
6×4=24通り
このなかで、AB BAのように、2本ずつだぶっているから
24÷2=12通り
リス だから、6つの点から2つ選べばいいんじゃないの
6C2=6×5÷(2×1)=15通り
これから、AB,CD,EFの3本を引いて
15-3=12通り
ウサギ いろいろな方法があるね。
次の問題へ進む