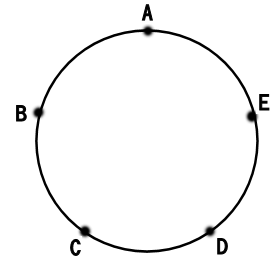
下の図のように、円の上に5つの点があります。
これらの5個の点のうち
3個の点を頂点とする三角形は,全部で何個できますか。
これらの5個の点のうち
3個の点を頂点とする三角形は,全部で何個できますか。
正解です 正解は10通りです。
マ ネットで樹形図を書くのは面倒だから樹形図だと思ってみてください。| A | B | C |
| D | ||
| E | ||
| C | D | |
| E | ||
| D | E |
次にAは除いて考えると、Bを選んだときは
B |
C | D |
| E | ||
| D | E |
次はABを除いてCを頂点にすると
C |
D | E |
足し算して、6+3+1=10通りだ
タヌキ
Aを選んだときは、残りの4つから2つ選ぶんだから
4×3÷2=6
と計算できるじゃない。
リス 5つの中から3つ選ぶんだから
5×4×3÷(3×2×1)=10通り
こうすれば簡単なのに。
平行線中の三角形