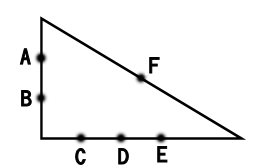
下の図のように、三角形の中に5つの点があります。
これらの5個の点のうち
3個の点を頂点とする三角形は,全部で何個できますか。
これらの5個の点のうち
3個の点を頂点とする三角形は,全部で何個できますか。
正解です 正解は19通りです。
リス 6つの点から3つ汚点を偉ぶって考えると
最初の点の選び方が、6通り。
2つめの点は、最初の点から一つ引いた5通りの選び方があって
3つめの点は、さらに一つ引いた、4通りの偉い方がある。
クマ 計算すると 6×5×4÷(3×2×1)=20通り
ウサギ そのうち CDEを選んだときは三角形にならないから
20-1=19通り
でできたね。
場合に分けてみると
クマ 点Aを頂点にすると残りの5つから2つ選ぶ方法は 5×4÷2=10通り
Aを抜かして、Bを頂点にすると
残りの4つから2つ選ぶ方法は 4×3÷2=6通り
ABをぬかして、Cを頂点にすると 3×2÷2=3通り
ABCを抜かしてDを頂点にすると 2×1÷2=1通り
タヌキ 全部足して 10+6+3+1=20通り
ウサギ そのうち CDEを選んだときは三角形にならないから
20-1=19通り
でできたね。
リス 同じような気がするけど。
2つのさいころ