平行線中の三角形

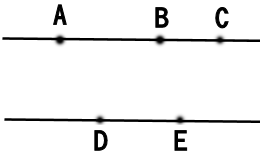
下の図のように、平行な2本の直線ア,イ上に
３個の点と2個の点がそれぞれあります。
これらの５個の点のうち
３個の点を頂点とする三角形は,全部で何個できますか。

正解です 正解は9通りです。


クマ　ABCに底辺があるとすると、
　　　　３つの点から２つ選べばいい。
タヌキ　樹形図を書くと
　　　　　A　　B
　　　　　　　　C
　　　　　B　　C
　　　　で２＋１＝３通り。（横線が引いてないけれど）
　　　　（計算ですると　３×２÷２＝３通り）
キツネ　その一つ一つに、頂点の取り方が、DとEの２通りあって・・・
タヌキ　だから、２×３＝６　通りある
クマ　次にDEを底辺があるとすると、これは１通り。
キツネ　頂点の取り方はA,B,Cの３通りあるから
　　　　　１×３＝３
ウサギ　これを足して　６＋３＝９通りだね。
リス　５つの点から３つ点を選ぶと
　　　　５×４×３÷（３×２×１）＝１０通り
　　　　ABCを選ぶと直線で三角形でなくなるから　１０－１＝９　でもいいね。
次は　三角形中の三角形