４枚のカードから

並べるというときは、並べる順番を考えて数えます。これを順列といいます。
今度は並べないで２枚選びます。
こんどは「A・B」と「B・A」を区別しないで考えます。
すると樹形図は、まず

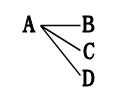
これで、Aのはいった組みあわせは全部です。
BーA　というのは、もうAーB　があるから、数えないということです。
だから、次は、Aはもう使いません。AとBとCだけで考えるのです。
すると、

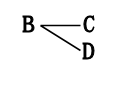
の２通りとなります。
これで、Bをつかったカードの組み合わせはもうありません。
AとBを除いた、CとDだけで考えます。
すると

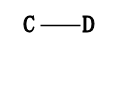
これで最後です。
全部で６通りになります。
３＋２＋１ で計算できますね。

計算の仕方は

では、計算ではできないでしょうか。
それには、次の計算を使います。

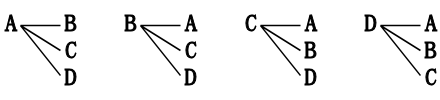
これは、順番を考えて、つまり、A-BとB-Aを区別して計算しました。
その計算は　４×３＝１２　でした。
ここでよく見ると
A-B と　B-A　というふうに、２つずつ組になっていることに気がつきます。
これは、ABの２界のカードの並べ方が２通りあるからです。
そこで、２枚ずつタブっているの半分にして
１２÷２＝６
と計算できるのです。
あれ、トーナメントと同じです。
トーナメントは、□チームから２チーム、順番を考えずに選び出すのと同じです。
４枚から２枚選ぶには
４×３÷２　で計算できるのです。

５チーム、トーナメント