円の回転

回転体の体積っていろいろな問題があるけれど、
今回はドーナツの体積を求める問題だ。
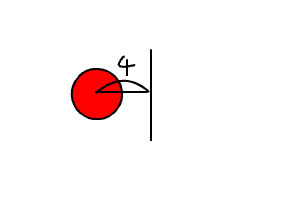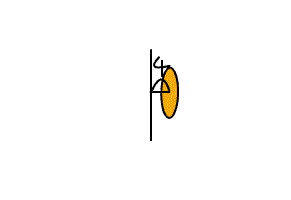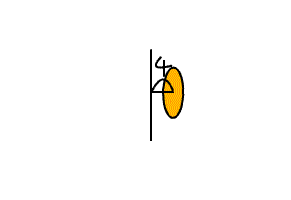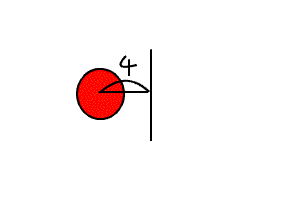
一本の線の周りを、下の図のように、
円が回転してできる面積を求めるにはどうしたらいいだろう。
まず、回転している円の面積は、円周率をπ（パイ）とすると
２×２×π＝４π
となる
円の中心は、半径４ｃｍの円の円周は、８π
そこでドーナツの体積は
４π×８π＝３２π~2
となります。
底面が４πで高さが８πの円柱の体積と同じなのですね。
ドーナツ型の体積＝円の面積×中心の描く円の円周の長さ
これは、パップス・ギュルダンの定理と言われています
回転体の体積と、円柱の体積が同じっておもしろいですね。
これは、積分をならうとよく理解できます。
（小学生６年生にこの話をしたら、
「小さい円の面積が沢山扱っているから・・・」
とたぶん直感的に理解してくれた。
中にはう～～んってうなる子もいたのかもしれないけど。
で、つぎは、もう一つの体積の話）
会社で使われている公式と平均断面法