コサインとは
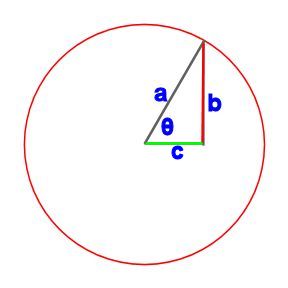
図のような直角三角形があったときa と c の角度がθ(シータ) のとき、 cos(θ) は c/a のことを表します。
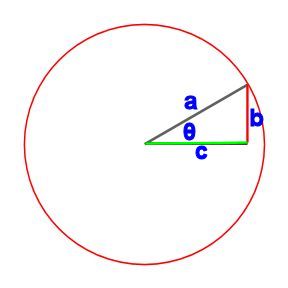
コサインのおぼえ方
cos(コサイン)のCは、次のように書きます。
そこで、コサインb/a(a分のb)は
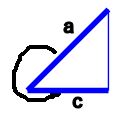
のようにして覚えます。
これは、a が1cmのときの、b の長さのことです。
どんな三角形でも、aが1cmのときの、cの長さが、角θ(しーた)を使ってcos(θ)として表せます。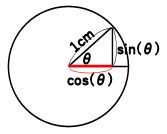
です。
aが10cmのときも、aはa÷10=1 と10で割ると1cmになり
bは sin(θ)=b/a と10で割ると、aが1cmの長さになります。、、
sin(θ)は、aが1cmのときのbの長さなのです。
半径が大きくなると
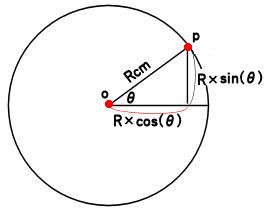
半径が大きくなってたとえばRcmになると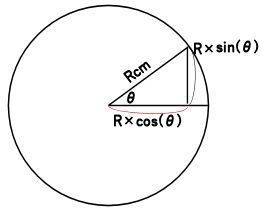
Cの長さは、Rcos(θ)と表せます。
点Pは
点Pの座標は、Rとθを使って(Rcos(θ),Rsin(θ))とあらわせます。
これまでの、(c、b)のように縦横の長さで表さなくて角度と、半径の長さであらさせるのです。
これをつかって、遠い星までの距離をはかっていました。
また、音とか電波も、このサインやコサインを使ってけ違算します。
θが大きくなると
a=1 のときθが0のときは、bは1になりますから sin(0)=1 です。
a=1 のとき
θが30度のときはsin(30) つまりbの長さは 約0.866

a=1 のとき
θが60度のときは sin(60) つまりbは 0.5
a=1 のとき
θが90度のときは sin(θ) は 0となります。
θが90度をこえると
θが90を超えると、sin(θ)はマイナスになりθが180になると、sin(180)はマイナス1になり
θが180を超えると、sin8(θ)はだんだん0に近づきます
なんだかよく分からない、使ってみましょう
まず定義から初期設定を作ります。
初期設定はいつも別で作っておくと、プログラムが見やすくなって便利です。
なんだサインと同じじゃないか・・・そうです。あとでサインといっしょに動かしたいのです。

つぎにこれですが
サインを少し変えただけです。
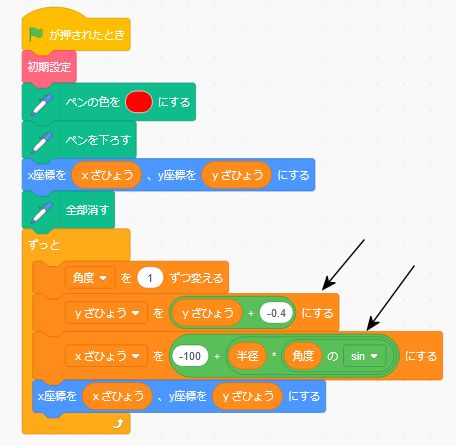
(★x座標を0にしておけば、[x座標を 半径×角度のsin]とするだけでいいね。)
試してみましょう
スプライトが、右に行ったり左へ行ったりしています。+1と-1の間を行き来しているのです。
これとsin(サイン)を使うときれいな円が描けます。
次は円をかいてみましょう。
円へ