かけ算のかける順番は
かけられる数とかける数の順番を逆にしてはいけないか
開け算の順番を逆にしたら×なのか○なのかという論争があって
○なのか×なのかはたして△なのか
さてどうして逆にして良いのか悪いのか、果たして同じなのか、
さて・・・
ひっくり返していいのか
最初から権威の説を持ち出すのは・・・はばかられるんだけど・・・出しちゃいますと・・・森 毅がこれについて書いている。僕はこれを四〇年ほど前に読んで・・・
(著書を探しています。 →書籍名を見ていたら、思い出しました→ 数の現象学 森毅 朝日選書、または 筑摩学芸文庫)
ここから一部引用します。
次元を異にする3種の乗法66p~80p の67pより
-----------------------以下引用--------------------------
…実は少しもかけ算の意味を教えていなかったところが小学校の問題なのだが、親の方にもいくらかヘンな
ところはある。…
…むしろ、乗法では交換法則が成立するのは特別で、なぜここで交換法則が成立するかが問題になる。
いまの親の説明というのは、交換法則を説明しているのである。もっとも、大学入試などだと、例えば次
のように書かないと大減点されるのだが、「一人に一個ずつくばると6人に対して6個必要になる。
一人あたり4個にするためには、それを四回繰り返さなければならない。
6個/回×四回=24個
つまり
4個/人×6人=24個
と言う最初の問題の6人を6個/回に、4個/人を四回に展開するということを書かないとオ、それぞれに1割程
度の原点を覚悟しなければならない
…中略…
さしあたり×は問題のある印だが…
----------------------引用終了--------------------------
やっぱり全体を読んでいただかないと、いけないのだろうが、かけ算の順番を考える上での
基礎資料の一つということであげておきます。
なお、もりの学校ではこんなページもあります
じゅんばんをいれかえたかけざん
交換できることも、きちんと教えるということで、作成したページです。
足し算で考えると
一あたりの量×いくつ分 5個/一皿×4皿 について 以下小学生でもかけ算の順番をどうして逆にして良いかと言うことを考えると(その1)
(ネコが5ヒキ入ったふくろが3つ 5+5+5 5が3つを 5×3 と書きます。
さてではこれは、3匹入った袋が5つ、3×5と同じでしょうか。
それには、5×3が3×5に変化することを示せばいいのでしょう。
そこで
どのふくろからも一ぴきずつとりだして、はこにいれます。
すると5ヒキ入りのハコが1つでkます。
もういちどふくろから1ぴきずつとりだして、はこにいれると
また、5ヒキ入りのハコができます。
もういちどふくろから一ぴきずつとりだして、はこにいれます。
これで5ヒキ入りのハコが3つできました。
ネコの数は 5+5+5 で 5ヒキ×3 と計算できます。
こうして
5×3 は 3×5 にもなるのです。)
こうして、答えは同じです。
ひっくり返すにはこうして遠回りをしなければいけない。
同じではない。
でも感覚的に分かってしまう子もいる。
ではどうするか。
(マルかバツか、これは又別の問題になってきます。)
かけ算の順番をどうして逆にして良いかと言うことをもう少し考えると(その2)
N×Mを考えると
N=1+1+1+1+ ・・・・・・・・・・ +1(N個の1)
N=1+1+1+1+ ・・・・・・・・・・ +1(N個の1)
N=1+1+1+1+ ・・・・・・・・・・ +1
・・・・・・・・・・
・・・・・・・・・・
・・・・・・・・・・
N=1+1+1+1+ ・・・・・・・・・・ +1
NがM個ある。
これがN×M
これを縦に見てみると
最初の1がMこ、2番目の1がMこ・・・・N番目の1がMこあります。
つまり、M+M+M+・・・・・・・・+M (MがN個)だから、M×N
こうして
N×M=M×N
になります。
かけ算の順番をどうして逆にして良いかと言うことを数学で証明すると(その3)
上のことをちゃんと数学的にやると証明ができると、ネット上にこの説明がありました。
比で考えると
イチゴ5個×4(倍)=20個 について以下小学校でのかけ算は足し算ではなくて、こっちで最近は教えているのが普通。
5×4=5×3+? なんてことも、足し算ふにおしえるけど。
かけ算を足し算で考えるんじゃなくて比で考えると
でも、かけ算は足し算で考えるのはちがうんじゃないか、3+3+3+3+3=3×5
と言うけれど+は4回しかないじゃないか5回はないぞ。
で、いろいろな対処法があって
0+3+3+3+3+3=3×5 と原点から比のように考える。
かけ算は比で考えたほうがいいと言う意見がどこかにあった。
ということで、 下のグラフで 5×2 と2×5を図にすると
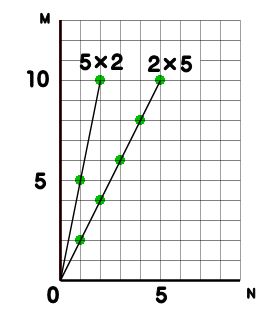
とちがった場所を指しています。
2つのかけ算は、別の意味があるということです。
でも答えは10で同じです。
これが同じことを比で証明するには・・・どうしたらいいんだろう・・・・
面積で考えれば逆になる
面積で考えれば、縦横ひっくり返しても同じじゃないか、という意見もあります。図は縦も横の対象で、単位も同じだから、交換しても良い。
図にしてみましょう。
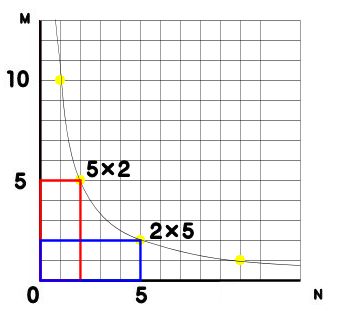
5×2の面積と2×5の面積はちょうど反比例の関係になります。
さて、さて同じは同じ10なのですが・・・・反比例上のちがう点です。
でも、面積でかけ算を表すのは便利で、もりの学校でもよく利用させてもらっています。
直感的にひっくり返しても同じだと分かります。
かけ算のこうかん
かける順番とかけ算
もう一つ 3+3+3+3+3=3×5 の説明に
3×5は、やはり足し算は4つしかないじゃないという考えにたいして箱に入れて図で説明する方法もある
タイルはいくつ
足し算も大切
かけ算と足し算
これは、足し算で教えるのではなくて、 3が5つある、3の5倍が3×5何だという方向の物です。
英語は逆に言うじゃないか
5の2倍を日本語では ご・かける・に といいますが
英語では、ツー・タイムズ・ファイブ、といいます。
ひっくり返っているじゃないか
というのはその国の言語の方言で、「私は学校へ行きます」が「私はいきます学校へ」というようなもの。
どちらが正しいというわけではなくて・・・その国はそれが正しいということです。
その国で逆に言ったら変になるだけです。(日本語は順番は割と融通が利く言語だと思います。)
逆にすると困るのか
自然数の掛け算は逆にできる。でもベクトルの掛け算(外積)は交換できない。b×a=-a×b でもそれは外積であって積じゃない・・・のか・・・
僕はこれを昭和の40年頃教わったときのこと
数学の先生は「ベクトルの外積は交換できない」と言って、僕は頭が真っ白になった、
その後、計算してみせてくれたけど、意味が分からなかった・・・
(四十数年前の話・・・今は丁寧に教えてくれるのでしょうけれど・・・)
かける数とかけられる数は最初から区別した方が良いんじゃないかと。。。個人の一例でどうのこうの言えることじゃありませんが。
その上で交換できることを教える・・・・
速さとかけ算
速さ×時間=距離距離÷時間=速さ
距離÷速さ=時間
この三つは面積とちがって、かける数とかけられる数の単位がちがっています。
世の中では、「はじき」なんていって計算をただの計算方法にしてしまう考えもありますが、きちんと意味理解をした方が良いと僕は思います。
このイメージは、かけ算のイメージで、
かけられる数を速さ(一単位時間に進む距離)に、かける数を時間に、全体を、距離とするとイメージしやすいのです。
かけられる数を1皿のおまんじゅうに、かける数をお皿の酢に、全体を全具のおまんじゅうに、と言うのとよく似ているのです。
距離を一秒の距離(速さ)で分ければ、時間が出る。
126メートルを秒速7メートルで進むと18秒かかるというイメージ
|
÷ |
|
= | 126m | |||
| 126m | |
| 7 | ×18 |
|
|||||||||||||||||||
|
|||||||||||||||||||
ただ「はじき」なんていう意味をのぞいた計算方法にしてしまえば、かける順番は変わりませんが、それでは速さの理解が進みません。
でも、速さのイメージを比例と捉えたらどうだろう。
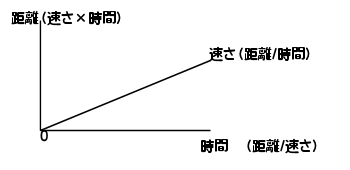
もっと先には、にはこのイメージなんだろうけれど、時間=距離÷速さ ってのが、上の説明の方が私はピンとくる。
これにするなら、時間×(1/速さ)って方がピンとくる。
さてさて、どこまで、どの学年であつかうのだろう。で、やっぱりかけられる数とかける数は別物かと思う。
ヘイズ朝の学習は、まず速さのイメージを作ることが大事だということで様々な実践がなされています。
(参考文献、力と運動・速さと距離と時間(事業書研究双書 15000円するんだ) 局地方程式のテキスト)
速さがよく分かってない人もいると思うけど、かけ算から引きずっている問題じゃないだろうか。
他のかけ算について
(以下書きかけ)行列式のかけざんは交換法則の成り立たない場合もある・・・・
電流と電圧、ワットとボルト、等などはどうイメージするんだろう。
どれが先なんだろう・・・・
というように、かけ算の順番問題は、ずっと今後の学習につながっている問題を含んでいるとは思うのです。
これに対する意見・・・・(以前読んだ書籍、誰か対談にあった気がするけど、これも探している最中です 何しろ40年前・・・)
(大分書籍を処分したからなぁ → 数学の世界:中公新書:森毅・竹内啓 P75 にありました。)
竹内さんは、交換しても良いんじゃないの、森さんはそれは少しちがう、という立場のようです。
世の中では逆に使われている例もあるのか
これをたくさん集めたら何か教材ができるかも知れないと集め始めた。ぼくも逆さまに使っていることがある(例えば 鶴亀算で・・・)
つるかめ算 基礎 の→ だいたいの見当をつけてみたらどう。
どうしてこうなるかは、更に考察が必要です。
これについては、算数数学とは離れるのかな・・・要検討。
注射液のビン1個から4人分の注射の液がとれる
注射液のビビン200個あったら何人分になるかというとき、200×4 も自然か気がする。
さて、これは、「一あたりの量×いくつ」っていうのお反対じゃないか。
これについたらどう考えたら良いのか。
算数ではない他の要素も入ってくるのか、さて、どこから丸にするのか、悩ましい問題が起きてくる。
これについては、もう少し考えたい。
ではマルかバツか
まるかばつかは単純に割り切れないと考えています。。
単に×とするのは、ちがうと思います。
○かというとそうでもなくて、回り道しているから多少減点
どうしてかというとの説明が必要です。
程度の立場でいます。
ここまで書きかけのページですが、途中公開です。
これから追記し、書き換えていきます。
突っ込みどころはたくさんあると思いますが・・・どこかで何かを書くと言いましたのでかいておきます・・・・
以上書きかけページで、今後改定していきます
感想、エラー報告のお願い
ぜひ、ご協力お願い申し上げます。