くま・・・表にしてみよう。
| 辺(へん) | 頂点(ちょうてん) | 面(めん) | 面+頂点-辺=2 | ||
| 直方体 ちょくほうたい |
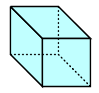 |
12 | 8 | 6 | 6+8ー12=2 |
| 三角錐 さんかくすい |
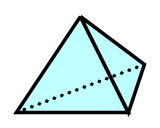 |
6 | 4 | 4 | 4+4ー6=2 |
りす・・・でどういうきまりがあるの。
くま・・・はい、ではきまりです。
オイラーの多面体定理(ためんたいていり)といいます。
りす・・・名前はどうでも良いよ、できまりは
くま・・・「面の数」+「頂点の数」-「辺の数」=2 となっています
りす・・・え~~本当(ほんとう)?
くま、いろいろの立体でためしてみてね。
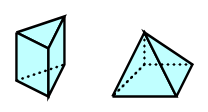
りす・・・え~~どうしてそうなるの~~~
くま・・・それは
辺・頂点・面の数とオイラーの多面体定理