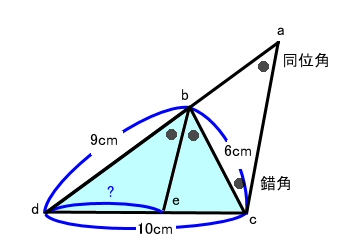
線分beに平行で点cを通る線を引きます
また、線分dbを伸ばします。
二本の線が重なったところをaとすると、
∠dbe=∠bac(同位角)
∠bca=∠bac(錯角)
そこで、三角形bacは二等辺三角形になって
線分ba=線分bc=6cmです
そこで、線分da=9+6=15cm
線分da:線分db=線分dc:線分deより
15:9=10:□
これを計算して□=6だから、de=6cm
となります。
bd:bc=de:ce
すると、ce=10-6=4 となります。bd:bc=9:6=3:2
また
de:ce=6:4=3:2
おや、同じです。
角dの二等分線は、dcを斜辺の長さの比に分けるのです。
この説明は次の問題でしてみましょう。直角三角形の長さ