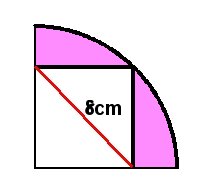
扇形の中心に重なるように、正方形が描かれています。
正方形の対角線は8cmです。
色を塗った部分の面積を求めなさい。
円周率は3.14とします。
正方形の対角線は8cmです。
色を塗った部分の面積を求めなさい。
円周率は3.14とします。
中の正方形の面積は
どうやって、色を塗った部分の面積を求ようか。
正方形の面積と、扇形の面積がわかれば、扇形の面積ー正方形の面積で、色をぬった面積がわかるよ。
正方形の面積は求められるだろうか。
対角線の長さが8cmだけれど、対角線がわかっても、縦や横の長さが分からないと面積は出ないよ。
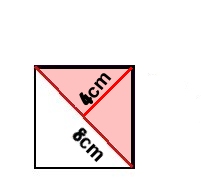
面積は三角形に分けてみればわかるって勉強したよね、三角形に分けてみようよ。
そうすると・・・あ、分かった、底辺8cm高さ4cmの三角形が2つと同じなんだ。
そうすると、正方形の面積は、8×4÷2×2=32平方センチメートルだ。
円の面積から引いて
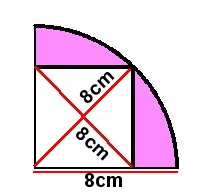
扇形の面積は、円の面積の4分の1だね。
円の面積は半径が分からないと分からないよ。
半径の長さは・・・・そうか、対角線と同じだから8cmだ。
そうすると、扇形の面積は、8×8×3.14÷4=50.24平方センチメートルだね。
さから、50.24-32=18.24平方センチメートル
できた~~~
次は
円と正方形の関係はおもしろい。
でも、これにもパターンがあって、1つ考えておくと、後の問題はどんどん解ける。
この問題が解ければ次も簡単に解けるだろう。
円の中の正方形
そして、その次が円の中の三角形の問題
円の中の三角
どこから初めても良い、こういう問題の積み重ねが、様々な解き方を身につけることになる。
その結果が、頭が柔軟だということになる。
頭が柔軟ということは、実は、たくさんの解き方を楽しんだ結果、賢くなっているということなのだ