回転してできる面積

円周率は３．１４とします。

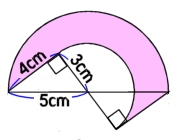
クマ　三角形を求めてから・・・・う～～ん。

移動すれば

リス　上の図のピンク色の面積は下の図のピンク色の面積と同じだ。

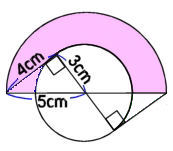
長さを入れて書き直してみるとこうなる。

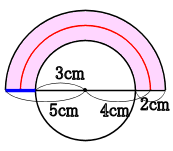
図は、青い線が回転してできた面積だといえる。
赤い線は、青い線の中心が回転して動いたところだ。
このとき、青い線の長さ×赤い線の長さで面積が出る。
青い線の長さは５－３＝２ｃｍ
赤い線は、半径４ｃｍ、ちょっけい８ｃｍの円の半分の長さだから
赤い線の長さ＝８×３．１４÷２＝４×３．１４ｃｍ
青い線×赤い線＝２×４×３．１４＝８×３．１４（ｃ㎡）
として面積が出る。
同じようにして体積を考えたもので、パップス・ギュルダンの定理というのもあります。
回転でできる面積３