0を中心にした、2重の半円の土地があります。
この黄色い色をぬった土地の面積は何㎡でしょう。
円周率を3.14またはπとして計算しなさい。
この黄色い色をぬった土地の面積は何㎡でしょう。
円周率を3.14またはπとして計算しなさい。
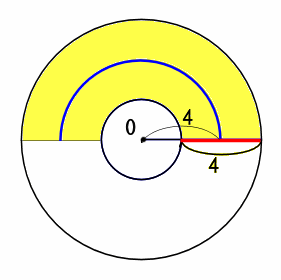
半円の面積は、赤い線と青い線の長さをかけると、出ます。
大きい半円から大きい半円を引いた赤い線の4mと、赤い線の中心の4mのところから書いた半円の長さをかけたものと等しいのです。
やってみましょう。
4÷2=2ですから、中間の青色で示した半円の半径は4m。直径は4×2=8m
半円の円周は、8×3.14÷2=4×3.14m
これと、4mをかけて
4×3.14×4=16×3.14
πを使って表すと16π
ほら先ほどの計算と同じになった。
これは、円の面積を求めたときの最後の考えと同じですね。
細く切って積み重ねれば、長方形になるのです。
これを、中線の定理といいます。
この考え方は立体の体積にも使えるでしょうか?
次は回転してできる面積1 三角形を見つけよう2