(問9/9)
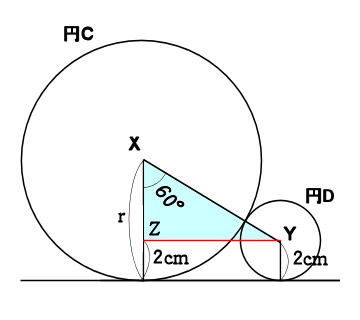
下の図において、点X、Yはそれぞれ円C、円Dの中心とします。
円Dの半径が4cmで、角Xの大きさが60°のとき、円Cの面積を求めなさい。
ただし円周率はπとし、円Cの半径は4cmより大きいものとします。
別の図を使って考えマ書言う。
xz:xy=1:2=r-2:xy
xyをrや2を使って表しましょう。
下の図において、点X、Yはそれぞれ円C、円Dの中心とします。
円Dの半径が4cmで、角Xの大きさが60°のとき、円Cの面積を求めなさい。
ただし円周率はπとし、円Cの半径は4cmより大きいものとします。
別の図を使って考えマ書言う。
xz:xy=1:2=r-2:xy
xyをrや2を使って表しましょう。

正解です。 正解は r+2 です。
水色の三角形で
xz:xyの比は
1:2= r-2:r+2
となります。
これを解くには、外項の積は内項の積に等しいという中学で今は習う非の説きをしないとダメですが
やってみましょう
まず、比の外側と外側、内側と内側をかけます
1×(r+2)=2×(r-2)
()を外すと
r+2=2×r+2×2
計算して
r+2=2×r-4
左右を入れ替えて
2×r-4=r+2
両辺からrを引いて
r-4=2
両辺に4を足して
r=2=4
=6
と計算します。半径が6と計算できます。
合格です。おめでとう
次の問題へ進む