(問6/9)
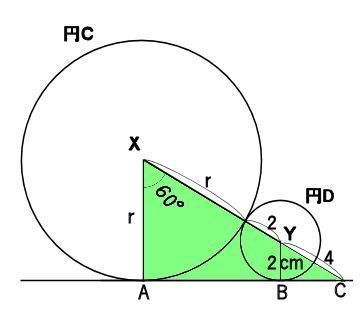
下の図において、点X、Yはそれぞれ円C、円Dの中心とします。
円Dの半径が2cmで、角Xの大きさが60°のとき、円Cの面積を求めなさい。
ただし円周率はπとし、円Cの半径は2mより大きいものとします。
辺XCの長さを、r,πや数字をつかって表しましょう。
下の図において、点X、Yはそれぞれ円C、円Dの中心とします。
円Dの半径が2cmで、角Xの大きさが60°のとき、円Cの面積を求めなさい。
ただし円周率はπとし、円Cの半径は2mより大きいものとします。
辺XCの長さを、r,πや数字をつかって表しましょう。

正解です。 正解は r+6 です。
大きい円の半径がr
小さい円の半径が2
YCが4cmです。
これを足せば良いですね。
r+2+4=r+6
となります。
次の問題へ進む