(問5/9)
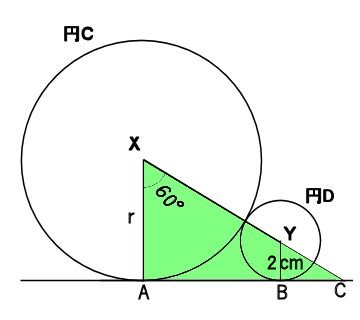
下の図において、点X、Yはそれぞれ円C、円Dの中心とします。
円Dの半径が2cmで、角Xの大きさが60°のとき、円Cの面積を求めなさい。
ただし円周率はπとし、円Cの半径は2mより大きいものとします。
辺yCの長さを、r,4,πをつかって表しましょう。
半径は r (アール)とかR(アール)を使って表すことが多いので、ここでもrを使っています。
下の図において、点X、Yはそれぞれ円C、円Dの中心とします。
円Dの半径が2cmで、角Xの大きさが60°のとき、円Cの面積を求めなさい。
ただし円周率はπとし、円Cの半径は2mより大きいものとします。
辺yCの長さを、r,4,πをつかって表しましょう。
半径は r (アール)とかR(アール)を使って表すことが多いので、ここでもrを使っています。
正解です。 正解は 2×2 です。
YCはYBの2倍ですから2×2=4cmになります。
次の問題へ進む