(問3/9)
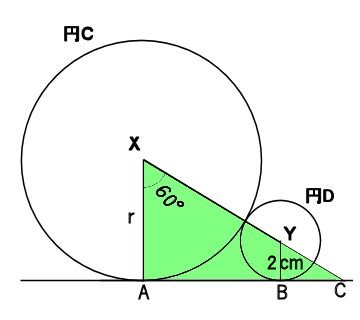
下の図において、点X、Yはそれぞれ円C、円Dの中心とします。
円Dの半径が2cmで、角Xの大きさが60°のとき、円Cの面積を求めなさい。
ただし円周率はπとし、円Cの半径は2mより大きいものとします。
xz:xy=1:2 になります。これはこの三角形を2つ合わせると正三角形になることから分かります。
下の図において、点X、Yはそれぞれ円C、円Dの中心とします。
円Dの半径が2cmで、角Xの大きさが60°のとき、円Cの面積を求めなさい。
ただし円周率はπとし、円Cの半径は2mより大きいものとします。
xz:xy=1:2 になります。これはこの三角形を2つ合わせると正三角形になることから分かります。
正解です。 正解は 1:2 です。
60度の直角三角形の辺の長さは次のようになっています。一番短い辺が1cmなら、一番長い辺は2倍の2cm
一番短い辺が2cmなら、一番長い辺は2倍の4cm
一番短い辺がxcmなら、一番長い辺は2倍の2xcmです。
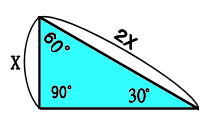
どうしてそうなっているかは、この三角形を2つくっつけて
正三角形を作ってみると分かるでしょう。
つまり
XA:XC=2:1
です。
次の問題へ進む