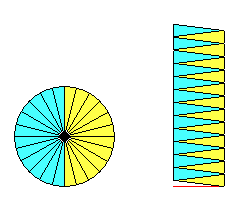
これらの図を描いたjavaプログラム(アプレットの紹介)
import java.awt.BorderLayout;
import java.awt.Color;
import java.awt.Graphics;
import javax.swing.JPanel;
import javax.swing.JApplet;
import java.awt.Dimension;
public class ensyuuMenseki extends JApplet {
private JPanel jContentPane = null; // @jve:decl-index=0:visual-constraint="10,9"
/**
* This is the xxx default constructor
*/
public ensyuuMenseki() {
super();
}
/**
* This method initializes this
*
* @return void
*/
int bunkaisu;
int r;
double startAngle; // 開始角度
double arcAngle; // 弧の大きさ
int xKijyun;
int yKijyun;
public void init() {
this.setSize(582, 505);
bunkaisu = 60; //円を6等分 ここを変更すれば分割数が変わる
r=200; //直径
startAngle = 180.0/(double)bunkaisu; ; //開始角度の絶対値
arcAngle = startAngle * 2.0; //弧の展開角度の大きさ
xKijyun=30; //基準点
yKijyun=260; //基準点
}
/**
* This method initializes jContentPane
*
* @return javax.swing.JPanel
*/
private JPanel getJContentPane() {
if (jContentPane == null) {
jContentPane = new JPanel();
jContentPane.setLayout(new BorderLayout());
}
return jContentPane;
}
public void paint(Graphics g ){
double rad = Math.toRadians(startAngle); //角度をラジアン値に変換
int x1=xKijyun;
int y1=yKijyun-r/2+(int)(Math.sin(rad)*(double)r/2) ;
int xp=(int)(Math.cos(rad)*(double)r/2)+r+10;
//長方形を描く
g.setColor(Color.red);
//g.drawRect(x1+xp , y1+r-(int)((double)r*Math.PI/2.0) , r/2 , (int) (((double)r*Math.PI)/2.0));
g.drawLine(x1+xp , y1+r-(int)((double)r*Math.PI/2.0)+(int) (((double)r*Math.PI)/2.0) , x1+xp+r/2, y1+r-(int)((double)r*Math.PI/2.0)+(int) (((double)r*Math.PI)/2.0));
g.setColor(Color.BLACK);
//円を分解して積み上げる
for(int i=0;i<bunkaisu;i++){
int plusY=(int)( Math.sin(rad) *r* (double)i /2.0);
int x=xKijyun;
int y=yKijyun-plusY;
int st=-1*(int)startAngle;
if(i/2*2 !=i){
st=180- (int)startAngle;
xp=(int)(Math.cos(rad)*(double)r/2)+r+10;
g.setColor(Color.CYAN);
g.fillArc(x+xp,y,r,r,st,(int)arcAngle);
g.setColor(Color.BLACK);
g.drawArc(x+xp,y,r,r,st,(int)arcAngle);
g.drawLine(x+r/2+xp , y+r/2 , x+r/2+xp-(int)(Math.cos(rad)*(double)r/2) , y+r/2+(int)(Math.sin(rad)*(double)r/2) );
if(i==bunkaisu-1)g.drawLine(x+r/2+xp , y+r/2 , x+r/2+xp-(int)(Math.cos(rad)*(double)r/2) , y+r/2-(int)(Math.sin(rad)*(double)r/2) );
}else{
xp=r+10;
g.drawLine(x+r/2+xp , y+r/2 , x+r/2+xp+(int)(Math.cos(rad)*(double)r/2) , y+r/2+(int)(Math.sin(rad)*(double)r/2) );
//g.drawLine(x+r/2+xp , y+r/2 , x+r/2+xp+(int)(Math.cos(rad)*(double)r/2) , y+r/2-(int)(Math.sin(rad)*(double)r/2) );
g.setColor(Color.YELLOW);
g.fillArc(x+xp,y,r,r,st,(int)arcAngle);
g.setColor(Color.BLACK);
g.drawArc(x+xp,y,r,r,st,(int)arcAngle);
}
}
//円を等分する
g.setColor(Color.YELLOW);
g.fillArc(x1,y1,r,r,0,360);
g.setColor(Color.CYAN);
g.fillArc(x1,y1,r,r,90,180);
g.setColor(Color.BLACK);
g.drawArc(x1,y1,r,r,0,360);
for( int i=0;i<bunkaisu;i++){
int stA=-1*(int)startAngle;
int arcA = (int)startAngle*i;
g.drawLine(x1+r/2 , y1+r/2 , x1+r/2+(int)(Math.cos(rad*i*2)*(double)r/2) , y1+r/2-(int)(Math.sin(rad*i*2)*(double)r/2) );
}
}
} // @jve:decl-index=0:visual-constraint="3,9"