半円と直角三角形

（問3/4）　
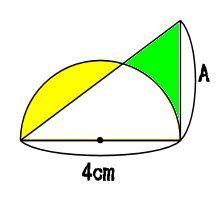
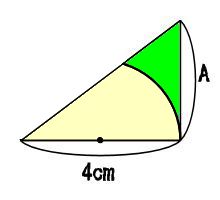
半円と直角三角形が重なっています。
黄色い部分の面積と、緑色の部分の面積は同じです。
Aで示した長さを求めなさい。
計算の簡素化のため、円周率は3.14ではなくて3とします。
図を二つに分けてみた。
これをヒントに、Aの長さを求めよう。

半円の面積は　半径×半径×3÷2　ですから
　2×2×3÷2=6c㎡です。

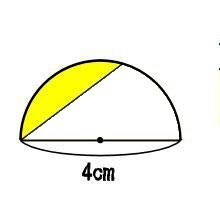
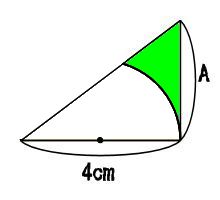
黄色と緑色の面積は等しいんだ

上の図駅それぞれに下の図形を加えると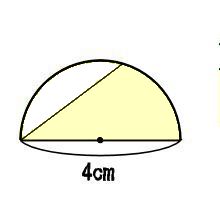

ほら、こうすると半円の面積と三角形の面積は同じになる。
同じ大きさを加えても面積の大きさは同じのままなんだ。

ということは三角形の面積は、6c㎡だろ。

この三角形の面積は６ｃ㎡
ということはAは
4×A÷2=6
2倍して
4×A=12
A=12÷4=3
と計算してAは３ｃｍになる

次の問題へ進む