多角形と円

（問　2/4）
三角形の頂点に、頂点を中心として半径４ｃｍの円が３つ書いてあります。
この円の水色の部分の面積を求めなさい。
円周率は３またはπとします。

正解です。　正解は 30,10π です。

水色の部分は何ｃ㎡ですか。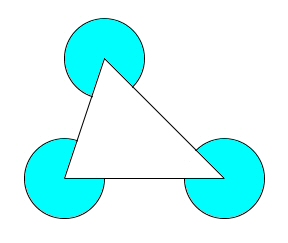

三角形の内角の和は１８０度です。
円は一回り３６０度。
だから欠けている円は、円の半分の大きさです。

３つの円から円の半分の大きさを引くと求める大きさになります。
円の半分が５つ分と考えても良いですね。
計算すると
２×２×３÷２×５＝（２×２÷２×５）×３＝３０　又は
２×２×π÷２×５＝１０π 答　３０ｃ㎡　または　１０πｃ㎡　です。
次の問題へ進む