下の図は1辺が1cmの正方形だとします。
面積は1c㎡です。
それでは、面積が個の正方形の2倍の正方形はかけますか。
面積は1c㎡です。
それでは、面積が個の正方形の2倍の正方形はかけますか。
(問2)
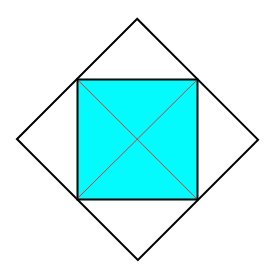
面積が2倍の三角形の1辺の長さは。
面積が2倍の三角形の1辺の長さは。
この数はどこまでいってのきりが無いことの説明:証明
この数は本当にきりがないのでしょうか。
それは、こうやって説明します。
--------------------------------------------
まず、この数があるとして、それをxとします。
すると x×x=2 となります。
| x= | b | ||
| a |
それが5桁で終われば、 10000分の何とかってすれば分数になりますね。
何桁でも、分数になります。
そして、この分数を、約分してもう約分できない数、a、bにしておきます。
さて、xを2つ掛け合わせると
| x×x= | b | × | b |
| a | a |
| x×x= | b×b | ||
| a×a |
| 2= | b×b | ||
| a×a |
ということは、bは2で割れます。bは偶数です。
そこで、bの変わりにb=2c (×を省略)とします。
これを①にいれると
2×a×a=2c×2c
2×a×a=4×c×c ・・・両辺を2で割ると
a×a=2×c×c
おや、aも2で割れます。
最初にaとbはもう約数はないようにしましたが
どちらも偶数で2で割れてしまいます。
これは、xがきりがある、つまり分数になるとしたのが間違いだから
ということは、xはきりがない、ということになります。
---------------------------------------
こういう説明を背理法といいます。
①あることを仮にあるとすると
②矛盾した結論が出る
③だから、仮にあるとしたことが間違っている
というわけです。
正方形の面積と対角線1