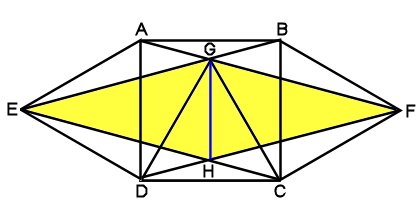
下の図は、正方形ＡＢＣＤ、正三角形ＡＢＥ、ＣＤＦを
組み合わせたものです。
ＡＦとＤＥの交点をＧ、ＢＦとＣＥの交点をＨとすると、
三角形ＢＣＧは正三角形になります。
ＡＢ＝３ｃｍのとき、四角形ＥＧＦＨの面積を求めなさい。
西大和学園中学 2010年
ＡＦとＤＥの交点をＧ、ＢＦとＣＥの交点をＨとすると、
三角形ＢＣＧは正三角形になります。
ＡＢ＝３ｃｍのとき、四角形ＥＧＦＨの面積を求めなさい。
西大和学園中学 2010年
正解です ９ｃ㎡です
ウサギ ＧＨに補助線を引くと三角形ＧＨＦ と 三角形ＧＣＦ の面積は同じだ。
そして、ＧＣ＝ＣＦ＝３ｃｍ
角ＧＣＦが９０°
だから、３×３÷２×２＝９ｃ㎡だね。
クマ どうして９０°なの
ウサギ ∠ＧＣＤ＝６０°
∠ＢＣＤ～９０°だから、引き算して
∠ＢＣＧ＝３０°
∠ＢＣＦ＝６０°だから
∠ＧＣＦ＝３０＋６０＝９０°だよ。
四角の中の四角
感想、エラー報告のお願い
ぜひ、ご協力お願い申し上げます。