(問2/2)
図のような面積が36c㎡の正六角形、ABCDEFがあります。
APの長さとBPの長さの比、
DQの長さの比、
ARの長さとFRの長さの比がすべて1:2、DSの長さとESの長さの比が1:1のとき、
次の面積をそれぞれ求めなさい。
東海中(2015)
{部分問題1}図のような面積が36c㎡の正六角形、ABCDEFがあります。
APの長さとBPの長さの比、
DQの長さの比、
ARの長さとFRの長さの比がすべて1:2、DSの長さとESの長さの比が1:1のとき、
次の面積をそれぞれ求めなさい。
東海中(2015)

図のように書くと、正三角形が左右に出来ます。
この△の面積は、36×(4/6)=24
FHを3等分、HEは2等分すると
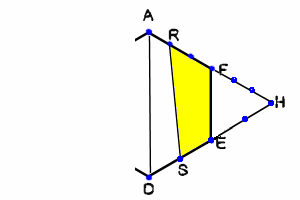
面積比で考えて
△AHD:△RHS:△FHE=6×4:5×3:3×2=24:15::6
△AHDの面積を20と考えると、
RFES=△RHS-△FHE=15-6=9 だから、
求める面積は、24×9/24=9 となります。
次へ進む