平行四辺形の面積比

東海中学　2001年(一部改訂）
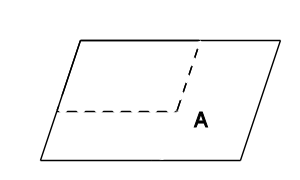
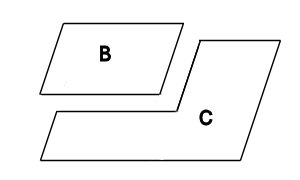
平行四辺形Aを何倍かに縮小した図形Bを作り、
AからBを下図のように切り取り、図形Cを作ります。
２つの図形BとCの周囲の長さを比べたところ、
Bの周囲の長さはCの周囲の長さは０．６倍でした。
このとき次の問に答えなさい。
（１）Bは元の平行四辺形Aを何倍に縮小したものですか。
（２）Bの面積が１２ｃ㎡のとき、Cの面積を求めなさい。

（２a）Bの面積とAの面積の比を求めなさい。

正解です　面積比は、５×５：３×３＝２５：９


BはAの０．６倍
ということは、縦も横も長さが０．６倍になっているということ
辺の比は　Aの辺：Bの辺＝１：０．６＝１０：６＝５：３だ。
辺の比が５：３なら面積比は、５×５：３×３＝２５：９　だ。
辺の比を2つ掛け合わせれば、面積の比になる。
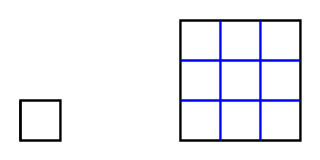
正方形で考えてみると、下の図のように、
辺の比が１：３だと、
面積の比は　１×１：３×３＝１：９　となる。

長方形で考えても三角形で考えても平行四辺形で考えても円で考えても、どんな図形で考えても
辺の比が　A:Bなら、
面積の比は　Ａ×Ａ：Ｂ×Ｂ　となるんだ。
次の問題へ進む