東海中学 2001年
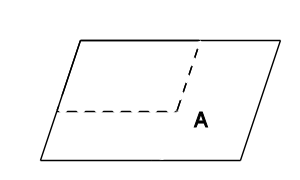
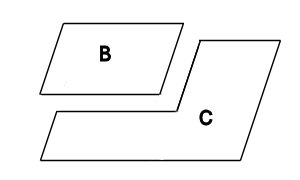
平行四辺形Aを何倍かに縮小した図形Bを作り、
AからBを下図のように切り取り、図形Cを作ります。
2つの図形BとCの周囲の長さを比べたところ、
Bの周囲の長さはCの周囲の長さは0.6倍でした。
このとき次の問に答えなさい。
(1)Bは元の平行四辺形Aを何倍に縮小したものですか。
(2)Bの面積が12c㎡のとき、Cの面積を求めなさい。
平行四辺形Aを何倍かに縮小した図形Bを作り、
AからBを下図のように切り取り、図形Cを作ります。
2つの図形BとCの周囲の長さを比べたところ、
Bの周囲の長さはCの周囲の長さは0.6倍でした。
このとき次の問に答えなさい。
(1)Bは元の平行四辺形Aを何倍に縮小したものですか。
(2)Bの面積が12c㎡のとき、Cの面積を求めなさい。
(1)Bは元の平行四辺形Aを何倍に縮小したものですか。
正解です
Cの図のへこんだところを膨らませればAの図になる。Cの周りの長さの0.6倍がB ということは
Aの周りの長さの0.6倍がB ということになる。
ということは、縦の長さも、横の長さも0.6倍。
答えはそのまま0.6倍だ。
次の問題へ進む