等分点と平行四辺形

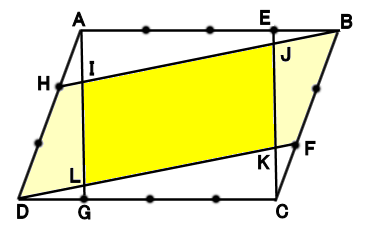
平行四辺形ＡＢＣＤがあります。
辺ＡＢ、ＣＤを４等分し、辺ＢＤ、ＤＡを３等分して図のように結ぶと
中に平行四辺形ＩＪＫＬができます。
中の平行四辺形ＬＪＫＬは外の平行四辺形ＡＢＣＤの何分のいくつでしょう。

（４）　中の平行四辺形ＬＪＫＬは外の平行四辺形ＡＢＣＤの何分のいくつでしょう。

正解です


辺ＢＪ：辺ＪＩ：辺ＩＨ＝３：９：１
ということは、台形ＩＨＤＦと台形ＪＩＬＫは高さが同じ三角形だから
面積は、底辺の長さの比になる。
つまり　３＋９＋１：９＝１３：９　だから
黄色い三角形は、平行四辺形ＢＨＤＦの９／１３になっている。
ＢＨＤＦは、外側の平行四辺形の２／３だから
２ × ９ ＝ ６
３ １３ １３
となる。
平行四辺形と三角形