平行四辺形と三角形２

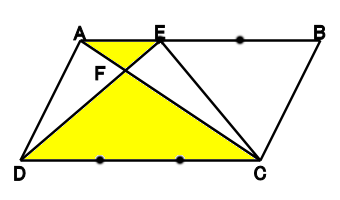
三角形ＡＥＦと三角形ＤＣＦは、
∠ＥＡＦ＝∠ＡＣＤ　で、∠ＡＥＦ＝∠ＦＤＣ　と２つの∠が同じですから
形は同じで大きさが違う三角形です。
こういう三角形を相似の三角形といます。
辺ＡＥと辺ＤＣを比べると、１：３です。
では、辺ＡＦ：辺ＦＣも同じように、１：３です。
辺ＡＦ：辺ＦＣも、１：３　です。
どの辺も３倍になっているのです。

もう一つの考え

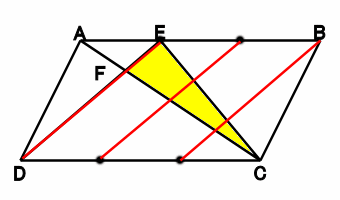
こんなふうに等間隔の平行線を引けば
AF*FC=１：３
ってすぐ分かる。
次の問題へ進む