(武蔵中学 2006)
四角形ABCDは、ADとBCが平行な台形で、
四角形ABEDはAB=6cmの平行四辺形です。
また、台形ABCDの面積は33c㎡、三角形ABCの
面積は24c㎡です。
(1)平行四辺形ABEDの面積を求めなさい。
(2)DFの長さを求めなさい。
四角形ABCDは、ADとBCが平行な台形で、
四角形ABEDはAB=6cmの平行四辺形です。
また、台形ABCDの面積は33c㎡、三角形ABCの
面積は24c㎡です。
(1)平行四辺形ABEDの面積を求めなさい。
(2)DFの長さを求めなさい。
正解です
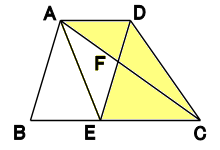
(2a)AF:FCの比を求めなさい
三角形CDA の面積は 9c㎡
三角形CDEの面積は平行四辺形から台形の面積を引けばいいから 33-18=15c㎡。
底辺がDCで共通な三角形だから、
高さの比は9:15=3:5となる。
だから、AD:EC=3:5 となる。
三角形ADFと三角形FEDは相似(同じ形)の三角形だから
AD:EC=AF:FC=DF:FE=3:5 です。
2つの三角形が相似であることはAD∥BCで (∥は∥という印)
∠ADE=∠CED
∠DAC=∠ACE
の2つの核が等しいことからいえます。
次の問題へ進む