(問2/2)
黄色い三角形と、平行四辺形ABCDとの面積の比を求めなさい。
なお平行四辺形は、一辺は2等分、もう一辺は5等分してあります。
黄色い三角形と、平行四辺形ABCDとの面積の比を求めなさい。
なお平行四辺形は、一辺は2等分、もう一辺は5等分してあります。
黄色い三角形と、平行四辺形ABCDとの面積の比を求めなさい。
なお平行四辺形は、一辺は2等分、もう一辺は5等分してあります。
黄色い三角形と、平行四辺形ABCDとの面積の比を求めなさい。
なお平行四辺形は、一辺は2等分、もう一辺は5等分してあります。
正解です。 正解は 1:5 です。

こんなふうに切ると、全部が20に切れます。
(4+1)×=2=20
そして、黄色い部分は。
4×1=4
です
だから
4:20=2:10=1:5
となります。
辺の比を長さのようにかけ算すると,面積の比がでます。
1:1の比をを高さのように考えるのです
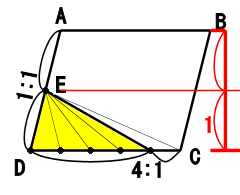
ほら、高さと同じ数と考えてもいいのです。
平行四辺形の面積比