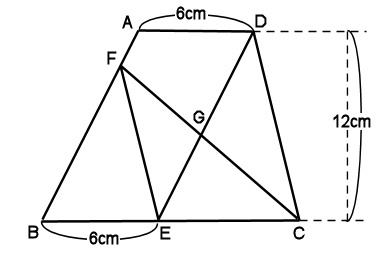
下の図のような台形ABCDがあり、
AD=BE=6cm、高さ12cmです。
CDとEFが平行で、
DE とCFの交点をGとしたとき、
DG:GE=5:4でした。
このとき、次の問に答えなさい。
(1)三角形EFGの面積を求めなさい。
(2)CEの長さを求めなさい。
(3)AF:FBを最も簡単な整数の比で表しなさい。
桐朋中学 2001年
(3)AF:FBを最も簡単な整数の比で表しなさい。
正解です 正解は1:4です。
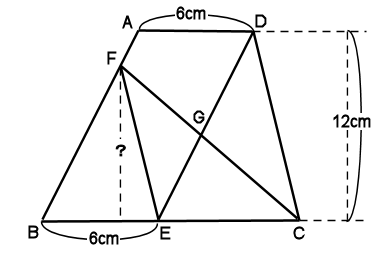
クマ ?の長さがわかれば、12-?:?が求める比とおなjになるね。
キツネ ECが、7.5cmで、三角形EFGが16c㎡、三角形GECが20c㎡.
タヌキ 三角形CEEの面積は、16+20=36c㎡
それを2倍して、EC=7.5cmで割って、?の長さは
36×2÷7.5=9.6cm
AF:FB=12-9.6:9.6=2.4:9.6=24:96=1:4:
リス 簡単になったね。
実は、△GFE:△GEC:△GCD=4×4:4×5:5×5=16:20:25 と比のかけ算で出るんだ。
前の問題もそうだったね、
正六角形と内部の面積