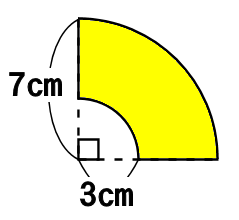
半径3cmの4分の1円と、
半径7cmの4分の一円が重なっています。
図の色を塗った部部の面積を求めましょう。
円周率は3.14とします。
半径7cmの4分の一円が重なっています。
図の色を塗った部部の面積を求めましょう。
円周率は3.14とします。
(問5)
円周率をπとするとどうなる。
円周率をπとするとどうなる。
これからの数学
これからは、3.14とかく代わりにπ(ぱい)とかきます。
横に線を引いて、その下に八のように書きます。
円周率は、3.14のあと、続きます。そしてきりのないことが分かっています。
そこで3.14とかく代わりに数学の世界ではπと書くのです。
すると色を塗った部分は
7×7×3.14÷4-3×3×3.14÷4
→7×7×π÷4-3×3×π÷4
となります。
みたところがよくなったでしょう。
そして、こういった文字のある式では、文字は後ろに書きます。
すると
→7×7÷4×π-3×3÷4×π
=(7×7÷4-3×3÷4)×π
| =(7×7× | 1 | ー3×3× | 1 | )×π | |
| 4 | 4 |
| =(7×7-3×3)× | 1 | ×π | |||
| 4 |
| =40× | 1 | ×π | |||
| 4 |
| =10 | ×π |
計算すると
=10×3.14
=31.4
ちょっと、数学の世界に触れましたが、
円周率や円の面積の学習では、もっと分配法則やπが使えるようになるよ。