({問3)
直方体の形をした水そうの中に、高さの等しい直方体を2個おいて階段を作ります。
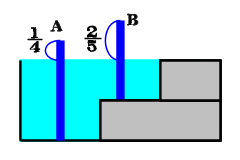
水槽の底面と、1段目に2本の棒 A,B をたてたところ
棒Aは、全体の4分の1、棒Bは、全体の5分の2だけ、それぞれ水面から上に出ました。
この2本の棒の和は、260cmのとき、2本の棒の長さを求めなさい。
直方体の形をした水そうの中に、高さの等しい直方体を2個おいて階段を作ります。
水槽の底面と、1段目に2本の棒 A,B をたてたところ
棒Aは、全体の4分の1、棒Bは、全体の5分の2だけ、それぞれ水面から上に出ました。
この2本の棒の和は、260cmのとき、2本の棒の長さを求めなさい。
今度は はこの高さを1とします。
すると、棒Aの長さは、水中にある部分は 1ー1/4=3/4で、水の深さは2ですから
2÷3/4=2×4/3=8/3(3分の8)になります。
、あた、棒Bの長さは、水中にある部分は 1ー2/5=3/5ですから
1÷3/5=1×5/3=5/3(3分の5)となります。
2つの棒の和は、
| 8 | + | 5 | = | 13 | ||
| 3 | 3 | 3 |
そこで、箱一段の高さは
| 260÷ | 3 | =60 | ||
| 13 |
| 棒A=120÷ | 3 | =120× | 4 | =160 | ||
| 4 | 3 |
| 棒B=60÷ | 3 | =60× | 5 | =100 | ||
| 5 | 3 |
次へ進む