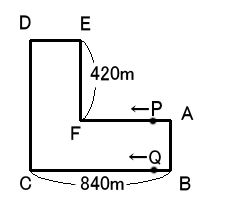
下の図のような通りがあります。曲がり角は全て直角でEF間は420m、BC間は840mです。PさんとQ君の歩く速さの比は4:5で、Pさんは時計と反対回りに、Q君は時計回りに道路上をもどることなく歩き続けます。
PさんがA地点から、Q君がB地点から、二人同時に出発した場合は、D地点で初めて出会います。このとき次の(1)(2)の問に答えなさい。
(1)この道路全体は、一周何mありますか。
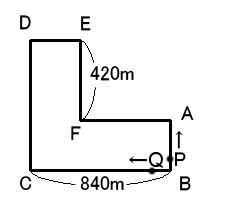
(2)PさんもQ君も、B地点から二人同時に出発した場合には、E地点で初めて出会います。A地点からF地点まで何メートルあるか求めなさい。
東邦大付属東邦中(千葉県)の問題より
PさんがA地点から、Q君がB地点から、二人同時に出発した場合は、D地点で初めて出会います。このとき次の(1)(2)の問に答えなさい。
(1)この道路全体は、一周何mありますか。
(2)PさんもQ君も、B地点から二人同時に出発した場合には、E地点で初めて出会います。A地点からF地点まで何メートルあるか求めなさい。
東邦大付属東邦中(千葉県)の問題より
まず(1)の問題から答えましょう。
(1)この道路全体は、一周何mありますか。
半周が 1575m になる。 一周が 3150mです。(2)PさんもQ君も、B地点から二人同時に出発した場合には、E地点で初めて出会います。
A地点からF地点まで何メートルあるか求めなさい。
一周が3150mです。
これを、5:4に分ければ、B→C→D→Eの長さと、B→A→G→Eの距離が出ます。
そこで、Pさんの歩く距離を□、Q君の歩く距離を△、とすると
PさんとQ君と全体の距離の比は
□:△:3150=5:4:9 です。
| □ | = | △ | = | 3150 |
| 5 | 4 | 9 |
| □ | = | 3150 |
| 5 | 9 |
| □= | 3150 | ×5=1750m |
| 9 |
そして、半周が、3150÷2=1575mですから、
DEの距離は、1750-1575=175mです。
そうするとA地点からF地点までは、840-175=665mです。
BCの長さが、840mだから、AFの長さは
840-175=665m です
ゆっくり1つずつ分かるkとから解いていけば、答えは出るんだね。
通過算のはじまり