キュリー夫人の問題を見て、いくつか似た問題を作ってみた。
1才や2才や3才は、3年前は生まれてないから、4才以上だ。
今何才かわからないから、□才と考えてみる。(□の変わりに、x を使う式も書いておくね)。
3年前の年令は、 □-3 才
3年前の年令を3倍すると (□-3)×3才 ・・・・・(1)
これが、3年後の年令と同じ。
3年後の年令は、□+3 ・・・・・・・・・・・・・・・・・・・・(2)
これが同じになればよい。
さて、□はどんな数字が入るだろう。□に数字をいれてみると
3才のときは
3年前は 3-0=0 これはどうにもならない
4才のときは
3年前は 4-3=1 3倍すると 3才、 3年後の年齢は 4+3=7才 差は4才
5歳のときは
3年前は 5-3=2 3倍すると 6才、 3年後の年齢は 5+3=8才 差は2才
6歳のときは
3年前は 6-3=3 3倍すると 9才、 3年後の年齢は 6+3=9才 差は0才
ということは、答えは6才

3年前の年齢を3倍したのと
今の年齢+3才と同じ
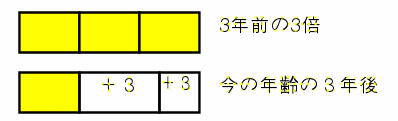
この2つを比べると、3年前の年齢の2倍は6才になる。
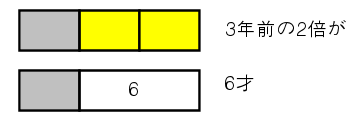
だから
2x=6
x=3
3年前3才だから、3+3=6才 これが答え
今の年れいを、x 才とすると
(x-3)×3=x+3
3x-9=x+3
2x=12
x=6
答え:6才
というふうになる。
3年前の年令の3倍が、3年後の年令と同じになるのは、
何才のときだろう。
何才のときだろう。
一つ目の考え方は
1才や2才や3才は、3年前は生まれてないから、4才以上だ。
今何才かわからないから、□才と考えてみる。(□の変わりに、x を使う式も書いておくね)。
3年前の年令は、 □-3 才
3年前の年令を3倍すると (□-3)×3才 ・・・・・(1)
これが、3年後の年令と同じ。
3年後の年令は、□+3 ・・・・・・・・・・・・・・・・・・・・(2)
これが同じになればよい。
さて、□はどんな数字が入るだろう。□に数字をいれてみると
3才のときは
3年前は 3-0=0 これはどうにもならない
4才のときは
3年前は 4-3=1 3倍すると 3才、 3年後の年齢は 4+3=7才 差は4才
5歳のときは
3年前は 5-3=2 3倍すると 6才、 3年後の年齢は 5+3=8才 差は2才
6歳のときは
3年前は 6-3=3 3倍すると 9才、 3年後の年齢は 6+3=9才 差は0才
ということは、答えは6才
もう一つの考え方は
3年前の年れいを x とすると x+3 が今の年齢
3年前の年齢を3倍したのと
今の年齢+3才と同じ

この2つを比べると、3年前の年齢の2倍は6才になる。

だから
2x=6
x=3
3年前3才だから、3+3=6才 これが答え
xを使って解くと
今の年れいを、x 才とすると
(x-3)×3=x+3
3x-9=x+3
2x=12
x=6
答え:6才
というふうになる。
もちろん3年前の年齢をxとしても解くことができる。
1年後の年令が1年前の3倍に